Fundamental Distributions

Univariate fundamental distributions¶

This section contains univariate fundamental distributions in the sense that they cannot refer to any other distribution -- only to functions, parameters and exactly one variable.

Argus distribution¶

The Argus background distribution is defined as

\[ \begin{aligned} \text{ArgusPdf}(m, m_0, c, p) = \frac{1}{\ensuremath{\mathcal{M}}} \cdot m \cdot \left[ 1 - \left( \frac{m}{m_0} \right)^2 \right]^p \cdot \exp\left[ c \cdot \left(1 - \left(\frac{m}{m_0}\right)^2 \right) \right] \end{aligned} \]

and describes the ARGUS background shape.

name: custom unique string
type: argus_dist
mass: name of the variable $m$ used as mass
resonance: value or name of the parameter used as resonance $m_0$
slope: value or name of the parameter used as slope $c$
power: value or name of the parameter used as exponent $p$.

Continued Poisson distribution¶

The of a continued Poisson distribution of the variable $x$ is defined as

\[ \begin{aligned} \text{ContinuedPoissonPdf}(x, \lambda) = \frac{1}{\ensuremath{\mathcal{M}}} \exp\left(x \cdot \ln \lambda - \lambda - \ln \Gamma(x+1)\right), \end{aligned} \]

where $\Gamma$ denotes the Euler Gamma function.

This function is similar the the Poisson distribution (see Poisson distribution{reference-type="ref" reference="dist:poisson"}), but can accept non-integer values for $x$. Notably, the differences between the two might be significant for small values of $x$ (below x). Nevertheless, the distribution is useful to deal with datasets with non-integer event counts, such as asimov datasets [^asymptotics].

name: custom unique string
type: poisson_dist
x: name of the variable $x$ (usually referred to as $k$ for the standard integer case)
mean: value or name of the parameter used as mean $\lambda$.

Uniform distribution¶

The of a continuous uniform distribution is defined as:

\[ \begin{aligned} \text{UniformPdf}(x) = \frac{1}{\ensuremath{\mathcal{M}}} \end{aligned} \]

name: custom unique string
type: uniform_dist
x: name of the variable $x$

CrystalBall distribution¶

The generalized Asymmetrical Double-Sided Crystall Ball line shape, composed of a Gaussian distribution at the core, connected with two powerlaw distributions describing the lower and upper tails, given by

\[ \begin{aligned} \text{CrystalBallPdf}(m;m_0,\sigma,\alpha_L,n_L,\alpha_R,n_R) = \frac{1}{\ensuremath{\mathcal{M}}} \begin{cases} A_L \cdot (B_L - \frac{m - m_0}{\sigma_L})^{-n_L}, & \mbox{for }\frac{m - m_0}{\sigma_L} < -\alpha_L \\ \exp \left( - \frac{1}{2} \cdot \left[ \frac{m - m_0}{\sigma_L} \right]^2 \right), & \mbox{for }\frac{m - m_0}{\sigma_L} \leq 0 \\ \exp \left( - \frac{1}{2} \cdot \left[ \frac{m - m_0}{\sigma_R} \right]^2 \right), & \mbox{for }\frac{m - m_0}{\sigma_R} \leq \alpha_R \\ A_R \cdot (B_R + \frac{m - m_0}{\sigma_R})^{-n_R}, & \mbox{otherwise}, \\ \end{cases} \end{aligned} \]

where

\[ \begin{aligned} A_i &= \left(\frac{n_i}{\left| \alpha_i \right|}\right)^{n_i} \cdot \exp\left(- \frac {\left| \alpha_i \right|^2}{2}\right) \\ B_i &= \frac{n_i}{\left| \alpha_i \right|} - \left| \alpha_i \right| \\ \end{aligned} \]

The keys are

name: custom string
type: crystalball_dist
m: name of the variable $m$
m0: name or value of the central value $m_0$
alpha: value or names of $\alpha_L$ and $\alpha_R$ from above. must not be used in conjuction with alpha_L or alpha_R.
alpha_L: value or names of $\alpha_L$ from above. must not be used in conjuction with alpha.
alpha_R: value or names of $\alpha_R$ from above. must not be used in conjuction with alpha.
n: value or names of $n_L$ and $n_R$ from above. must not be used in conjuction with n_L or n_R.
n_L: value or names of $n_L$ from above. must not be used in conjuction with n.
n_R: value or names of $n_R$ from above. must not be used in conjuction with n.
sigma: value or names of $\sigma_L$ and $\sigma_R$ from above. must not be used in conjuction with sigma_L or sigma_R.
sigma_L: value or names of $\sigma_L$ from above. must not be used in conjuction with sigma.
sigma_R: value or names of $\sigma_R$ from above. must not be used in conjuction with sigma.

Exponential distribution¶

The exponential distribution is defined as

\[ \begin{aligned} \text{ExponentialPdf}(x, c) = \frac{1}{\ensuremath{\mathcal{M}}} \cdot \exp(-c\cdot x) \end{aligned} \]

name: custom unique string
type: exponential_dist
x: name of the variable $x$
c: value or name of the parameter used as coefficient $c$.

Gaussian Normal distribution¶

The Gaussian/Normal distribution is defined as

\[ \begin{aligned} \text{GaussianPdf}(x, \mu, \sigma) = \frac{1}{\ensuremath{\mathcal{M}}} \exp\left(\frac{(x-\mu)^2}{\sigma^2}\right) \end{aligned} \]

name: custom unique string
type: gaussian_dist or normal_dist
x: name of the variable $x$
mean: value or name of the parameter used as mean value $\mu$
sigma: value or name of the parameter encoding the standard deviation $\sigma$.

Log-Normal distribution¶

The log-normal distribution is defined as

\[ \begin{aligned} \text{LogNormalPdf}(x, \mu, \sigma) &= \frac{1}{\ensuremath{\mathcal{M}}} \frac{1}{ x } \exp\left( -\frac{(\ln(x)-\mu)^2}{2\sigma^2}\right) \end{aligned} \]

name: custom unique string
type: lognormal_dist
x: name of the variable $x$
mu: value or name of the parameter used as $\mu$
sigma: value or name of the parameter $\sigma$ describing the shape

Poisson distribution¶

The Poisson distribution of the variable $x$ is defined as

\[ \begin{aligned} \text{PoissonPdf}(x, \lambda) = \frac{1}{\ensuremath{\mathcal{M}}} \frac{\lambda^x}{x!} \text{e}^{-\lambda}. \end{aligned} \]

where $x$ is required to be an integer. In this case, the behavior for non-integer values of $x$ is undefined. - name: custom unique string - type: poisson_dist - x: name of the variable $x$ (usually referred to as $k$ for the standard integer case) - mean: value or name of the parameter used as mean $\lambda$.

Polynomial distribution¶

The polynomial distribution is defined as

\[ \begin{aligned} \text{PolynomialPdf}(x, a_0, a_1, a_2, ...) = \frac{1}{\ensuremath{\mathcal{M}}} \sum_{i=0}^n a_i x^i = a_0 + a_1 x + a_2 x^2 + ... \end{aligned} \]

name: custom unique string
type: polynomial_dist
x: name of the variable $x$
coefficients: array of coefficients $a_i$. The length of this array implies the degree of the polynomial.

Multivariate fundamental distributions¶

This section contains multivariate fundamental distributions. They may refer to functions, parameters and more than one variable.

Barlow-Besston-Lite Constraint distribution¶

This distribution represents a product of Poisson distributions defining the statistical uncertainties of the histogram templates defined in a histfactory_func.

\[ \begin{aligned} \text{BarlowBeestonLitePoissonConstraintPdf}(x) &= \frac{1}{\ensuremath{\mathcal{M}}} \prod_i^n \text{PoissonPdf}(x_i\cdot \tau_i,\tau_i) \end{aligned} \]

name: custom unique string
type: barlow_beeston_lite_poisson_constraint_dist
x: name of the variable $x$
expected: array of central values $\tau_i$

Multivariate normal distribution¶

The multivariate normal distribution is defined as

\[ \begin{aligned} \text{MvNormalPdf}(\mathbf{x}, \boldsymbol\mu, \boldsymbol\Sigma) &= \frac{1}{\ensuremath{\mathcal{M}}} \exp \left( -\frac{1}{2} (\mathbf{x} - \boldsymbol\mu)^{\!\mathsf{T}} \boldsymbol\Sigma^{-1}(\mathbf{x} - \boldsymbol\mu) \right), \end{aligned} \]

with $\boldsymbol\Sigma \in \mathbb{R}^{k\times k}$ being positive-definite.

name: custom unique string
type: multivariate_normal_dist
x: array of names of the variables $\mathbf{x}$. This also includes mixed arrays of values and names.
mean: array of length $k$ of values or names of the parameters used as mean values $\boldsymbol\mu$
covariances: an array comprised of $k$ sub-arrays, each of which is also of length $k$, designed to store values or names of the entries of the covariance matrix $\boldsymbol\Sigma$. In general, the covariance matrix $\boldsymbol\Sigma$ must be symmetric and positive semi-definite.

Note: Users should prefer the specific distributions defined in this standard over generic distributions where possible, as implementations of these will typically be more optimized. Generic distributions should only be used if no equivalent specific distribution is defined.

A generic distribution is defined by an expression that respresents the PDF of the distribution in respect to the Lebesque measure. The expression must be a valid HS³-expression string (see Section Generic Expressions).

name: custom string
type: generic_dist
expression: a string with a generic mathematical expression. Simple mathematical syntax common to most programming languages should be used here, such as x-2*y+z. The arguments x, y and z in this example must be parameters, functions or variables. The distribution is normalized by the implementation, a normalization term should not be included in the expression. If the expression results in a negative value, the behavior is undefined.

HistFactory distribution¶

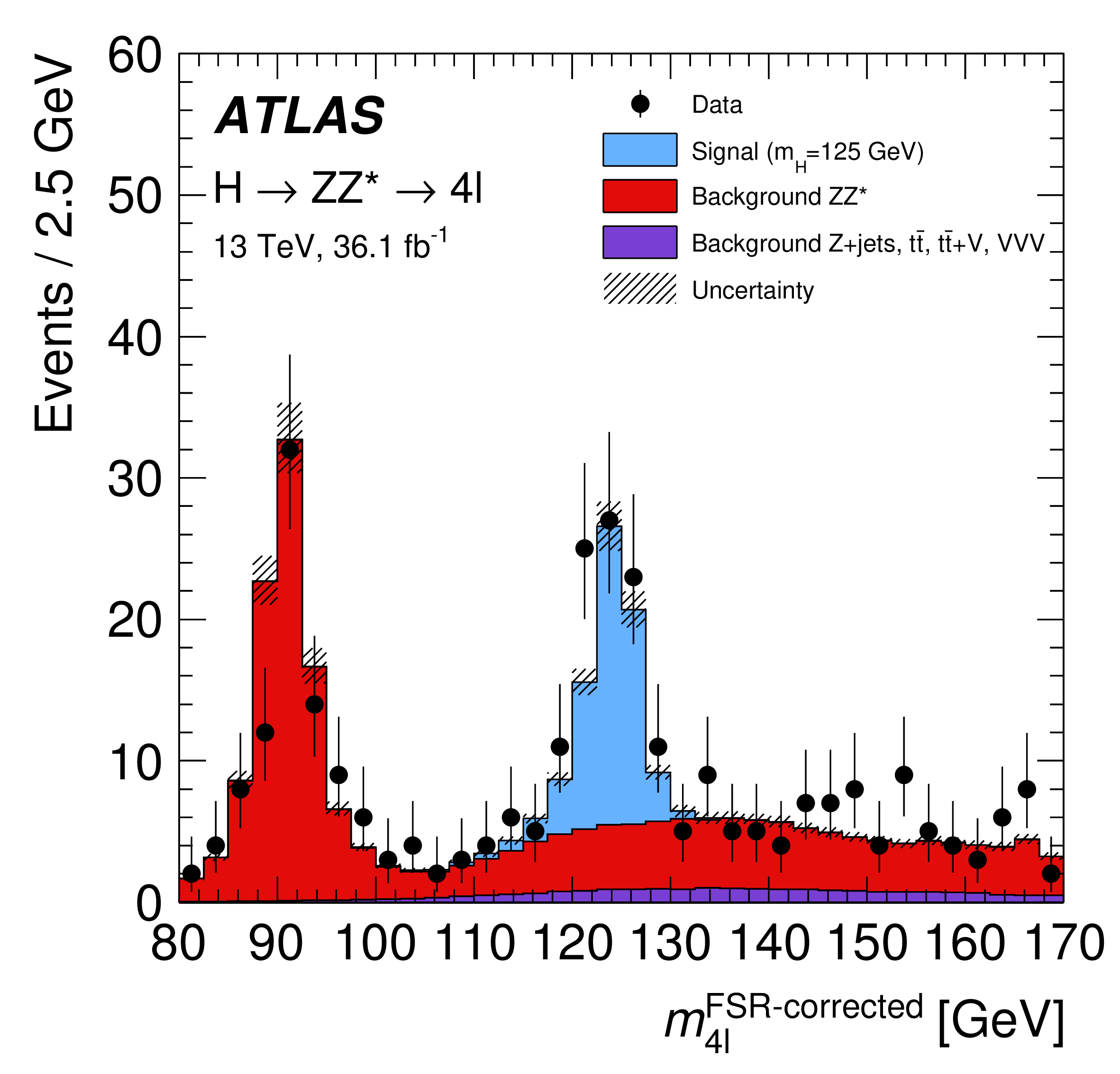
HistFactory [^hf] is a language to describe statistical models consisting only of "histograms" (which is used interchangeably with "step-functions" in this context). Each HistFactory distribution describes one "channel" or "region" of a binned measurement, containing a stack of "samples", i. e. binned distributions sharing the same binning (step-functions describing the signal or background of a measurement). Such a HistFactory model is shown in Figure 1 (originally from [^atlashzz]). Each of the contributions may be subject to modifiers.

$A binned statistical model describing a High Energy Physics measurement, in this case of the $H\rightarrow 4l$ process by the ATLAS collaboration. Three different sample (blue, red, violet) are considered.$

The prediction for a binned region is given as

\[ \begin{aligned} \lambda(x)=\sum_{s\in\text{samples}} \left[ \left( d_s(x) + \sum_{\delta\in M_{\delta}} \delta(x,\theta_\delta) \right) \prod_{\kappa\in M_\kappa} \kappa(x,\theta_\kappa) \right] \end{aligned} \]

Here $d_s(x)$ is the prediction associated with the sample $s$, a step function

\[ \begin{aligned} d_s(x) = \chi^{y_s}_{b}(x) \end{aligned} \]

In this section, $\chi^{y_s}_{b}(x)$ denotes a generic step function in the binning $b$ such that $\chi_{b}(x) = y_{s,i}$, some constant, if $x\in[b_i,b_{i+1})$. The $y_{s,i}$ in this case are the bin contents (yields) of the histograms. The $M_\kappa$ are the multiplicative modifiers, the $M_\delta$ are the additive modifiers. Each of the modifiers is either multiplicative ($\kappa$) or additive ($\delta$). All samples and modifiers share the same binning $b$. The modifiers depend on a set of nuisance parameters $\theta$, where each modifier can only depend on one $\theta_i$, but the $\theta_i$ can take the form of vectors and the same $\theta_i$ can be shared by several modifiers. By convention, these are denoted $\alpha$ if they affect all bins in a correlated way, and $\gamma$ if they affect only one bin at a time. The types of modifiers are

A uncorrelated shape systematic or shapefactor modifier is a multiplicative modifier that scales each single bin by the value of some independent parameter $\gamma$. Here, $\theta_i=\vec{\gamma}$, where the length of $\vec{\gamma}$ is equal to the number of bins in this region. This type of modifier is sometimes called shapesys, with some nuance in the meaning. However, both are synonymous in the context of this standard.
A correlated shape systematic or histosys modifier is an additive modifier that adds or subtracts a constant step function $\chi^f$, scaled with a single factor $\alpha$. The modifier contains a data section, which contains the subsections $\texttt{hi}$ and $\texttt{lo}$ that help to define the step function $\chi^f$. They contain contents, which define the bin-wise additions or subtractions for $\alpha=1$. Here, $\theta_i=\alpha$.
A normalization systematic or normsys modifier is a multiplicative modifier that scales the entire sample with the same constant factor $f$ that is a function of $\alpha$. The modifier contains a data section, which contains the values $\texttt{hi}$ and $\texttt{lo}$ that help to define $f$. There are different functional forms that can be chosen for $f$. However, by convention $f(\alpha=0)=1$, $f(\alpha=+1)=$"hi" and $f(\alpha=-1)=$"lo". In this case, $\theta_i=\alpha$.
A normalization factor or normfactor modifier is a multiplicative modifier that scales the entire sample in this region with the value of the parameter $\mu$ itself. In this case, $\theta_i=\mu$.
The staterror modifier is a shorthand for encoding uncorrelated statistical uncertainties on the values of the step-functions, using a variant¹ of the Barlow-Beeston Method [^barlowbeeston]. Here, the relative uncertainty on the sum of all samples in this region containing the staterror modifier is computed bin-by-bin. Then, a constrained uncorrelated shape systematic (shapesys) is created, encoding these relative uncertainties in the corresponding Poisson (or Gaussian) constraint term.

The different modifies and their descriptions are also summarized in the following table:

Type of Modifier	Description	Definition	Free Parameters	Number of Free Parameters
`histosys`	Correlated Shape systematic	$\delta(x,\alpha) = \alpha * \chi_b^f$	$\alpha$	1
`normsys`	Normalization systematic	$\kappa(x,\alpha) = f(\alpha)$	$\alpha$	1
`normfactor`	Normalization factor	$\kappa(x,\mu) = \mu$	$\mu$	1
`shapefactor`, `staterror`	Shape factor	$\kappa(x,\vec{\gamma}) = \chi_b^{\gamma}$	$\gamma_0$, ..., $\gamma_n$	#bins

The staterror modifier is a special subtype of shapefactor, where the mean of the constraint is given as the sum of the predictions of all the samples carrying a staterror modifier in this bin. The way modifiers affect the yield in the corresponding bin is subject to an interpolation function. The overallsys and histosys modifiers thus allow for an additional key interpolation, which identifies one of the following functions:

lin: $\begin{cases} y_{\textit{nominal}} + x \cdot (y_{\textit{high}} - y_{\textit{nominal}}) \text{ if } x\geq0\\ y_{\textit{nominal}} + x \cdot (y_{\textit{nominal}} - y_{\textit{low}}) \text{ if } x<0 \end{cases}$
log: $\begin{cases} y_{\textit{nominal}} \cdot \left(\frac{y_{\textit{high}}}{y_{\textit{nominal}}}\right)^x \text{ if } x\geq0\\ y_{\textit{nominal}} \cdot \left(\frac{y_{\textit{low}}}{y_{\textit{nominal}}}\right)^{-x}\text{ if } x<0 \end{cases}$
parabolic: $\begin{cases} y_{\textit{nominal}} + (2s+d)\cdot(x-1)+(y_{\textit{high}} - y_{\textit{nominal}}) \text{ if } x>1\\ y_{\textit{nominal}} - (2s-d)\cdot(x+1)+(y_{\textit{low}} - y_{\textit{nominal})}\text{ if } x<-1\\ s \cdot x^2 + d\cdot x \text{ otherwise} \end{cases}$ with $s=\frac{1}{2}(y_{\textit{high}} + y_{\textit{low}}) - y_{\textit{nominal}}$ and $d=\frac{1}{2}(y_{\textit{high}} - y_{\textit{low}})$
poly6: $\begin{cases} y_{\textit{nominal}} + x \cdot (y_{\textit{high}} - y_{\textit{nominal}}) \text{ if } x>1\\ y_{\textit{nominal}} + x \cdot (y_{\textit{nominal}} - y_{\textit{low}}) \text{ if } x<-1\\ y_{\textit{nominal}} + x \cdot (S + x \cdot A \cdot (15 + x^2 \cdot (3x^2-10))) \text{ otherwise} \end{cases}$ with $S = \frac{1}{2}(y_{\textit{high}} - y_{\textit{low}})$ and $A=\frac{1}{16}(y_{\textit{high}} + y_{\textit{low}} - 2\cdot y_{\textit{nominal}})$

Modifiers can be constrained. This is indicated by the component constraint, which identifies the type of the constraint term. In essence, the likelihood picks up a penalty term for changing the corresponding parameter too far away from its nominal value. The nominal value is, by convention, defined by the type of constraint, and is 0 for all modifiers of type sys (histosys, normsys) and is 1 for all modifiers of type factor (normfactor, shapefactor). The strength of the constraint is always such that the standard deviation of constraint distribution is $1$.

The supported constraint distributions, also called constraint types, are Gauss for a gaussian with unit width (a gaussian distribution with a variance of $1$), Poisson for a unit Poissonian (e.g. a continous Poissonian with a central value 1), or LogNormal for a unit LogNormal,. If a constraint is given, a corresponding distribution will be considered in addition to the aux_likelihood section of the likelihood, constraining the parameter to its nominal value.

An exception to this is provided by the staterror modifier as described above, and the shapesys for which a Poissonian constraint is defined with the central values defined as the squares of the values defined in vals.

The components of a HistFactory distribution are:

name: custom unique string
type: histfactory_yield
axes: array of structs representing the axes. If given each struct needs to have the component name. Further, (optional) components are max, min and nbins, or, alternatively, edges. The definition of the axes follows the format for binned data (see Section Binned Data).
samples: array of structs containing the samples of this channel. For details see below. Struct of one sample:
name: (optional) custom string, unique within this function
data: struct containing the components contents and errors, depicting the data contents and their errors. Both components are arrays of the same length.
modifiers: array of structs with each struct containing a component type of the modifier, as well as a component parameter (defining a string) or a component parameters (defining an array of strings) relating to the name or names of parameters controlling this modifier. Further (optional) components are data and constraint, both depending on the type of modifier. For details on these components, see the description above. Two modifiers are correlated exactly if they share the same parameters as indicated by parameter or parameters. In such a case, it is mandatory that they share the same constraint term. If this is not the case, the behavior is undefined.

HistFactory

{
  "name": "myAnalysisChannel",
  "type": "histfactory_dist",
  "axes": [ 
    { "max": 1.0, "min": 0.0, "name": "myRegion", "nbins": 2 } 
  ],
  "name":"myChannel1",
  "samples": [
    { 
      "name": "mySignal",
      "data": { "contents": [ 0.5, 0.7 ], "errors": [ 0.1, 0.1 ] },
      "modifiers": [
        { "parameter": "Lumi", "type": "normfactor" },
        { "parameter": "mu_signal_strength", "type": "normfactor" },
        { "constraint": "Gauss", "data": { "hi": 1.1, "lo": 0.9 }, 
          "parameter": "my_normalization_systematic_1", 
          "type": "normsys" },
        { "constraint": "Poisson", "type": "staterror", 
          "parameters": ["gamma_stat_1","gamma_stat_2"]},
        { "constraint": "Gauss", "type": "histosys", 
          "data": { 
            "hi": { "contents": [ -2.5, -3.1 ] }, 
            "lo": { "contents": [ 2.2, 3.7 ] } 
           }, 
           "parameter": "my_correlated_shape_systematic_1" },
        { "constraint": "Poisson", "data": { "vals": [ 0.0, 1.2 ] }, 
          "parameter": "my_uncorrelated_shape_systematic_2", 
          "type": "shapesys" }
      ]
    },
    { 
      "name": "myBackground",
      ... 
   }
  ]
}

Relativistic Breit-Wigner distribution¶

The relativistic Breit-Wigner distribution describes the lineshape of a resonance studies in the mass spectrum of two particle system. It is assumed that the resonance can decay into a list of channels.

The first channel in the list indicates the system for which mass distribution is modelled.

\[ \begin{aligned} \label{eq:relativistic_breit_wigner_dist} \text{BreitWignerPDF}(m, m_\text{BW}) &= \frac{1}{\ensuremath{\mathcal{M}}}\frac{m \Gamma_1(m)}{\left|m_\text{BW}^2-m^2 - i m_\text{BW} \Gamma(m)\right|^2} ,\\ \nonumber \Gamma(m) &= \sum_i \Gamma_i(m) ,\\ \nonumber \end{aligned} \]

When modelling the mass spectrum, the term $m$ in the numerator of Eq. (Breit-Wigner) accounts for a jacobian of transformation from $m^2$ to $m$. The width term $\Gamma_1(m)$ adds for the phase space factor for the channel of interest

name: custom unique string
type: relativistic_breit_wigner_dist
mass: name of the mass variable $m_\text{BW}$
channels: list of structs encoding the channels

Each of the channels is defined by the partial width $\Gamma_i(m)$, given as

\[ \begin{aligned} \Gamma_i(m) &= \Gamma_{\text{BW},i} n_{li}^2(m)\rho_i(m) ,\\ \nonumber \rho_i(m) &= 2q_i(m)/m ,\\ \nonumber q_i(m) &= \sqrt{(m^2-(m_{1i}+m_{2i})^2)(m^2-(m_{1i}-m_{2i})^2)} / (2m) ,\\ \nonumber n_{li}(m) &= z_i^{li}(m) h_{li}(z_i(m)) ,\\ \nonumber z_i(m) &= q_i(m)R_i \end{aligned} \]

The $h_l(z)$ is the standard Blatt-Weisskopf form-factors, $h_0^2(z) = 1/(1+z^2)$, $h_1^2(z) = 1/(9+3z^2+z^4)$, and so on (Eqs.(50.30-50.35) in Ref. [^pdg2023]).\ The structs defining the channels should contain the following keys:

name: name of the final state (optional)
Gamma: partial width $\Gamma_{\text{BW}}$ of the resonance
m1: mass $m_1$ of the first particle the resonance decays into (default value $0$)
m2: mass $m_2$ of the second particle the resonance decays into (default value $0$)
l: orbital angular momentum $l$ (default value $0$)
R: form-factor size parameter $R$ (default value $3$ GeV) For non-zero angular momentum, $\Gamma_i(m_\text{BW})$ gives an approximation to the partial width of the resonance, not $\Gamma_{\text{BW},i}$. A commonly used approximation of the relativistic Breit-Wigner function with the constant width is a special case of the Eq. (Breit-Wigner), where the [channels] argument contains a single channel with $m_1=0$, $m_2=0$, and $l=0$.

The variation consists of summarizing all contributions in the stack to a single contribution as far as treatment of the statistical uncertainties is concerned. ↩

Type of Modifier	Description	Definition	Free Parameters	Number of Free Parameters
`histosys`	Correlated Shape systematic	\(\delta(x,\alpha) = \alpha * \chi_b^f\)	\(\alpha\)	1
`normsys`	Normalization systematic	\(\kappa(x,\alpha) = f(\alpha)\)	\(\alpha\)	1
`normfactor`	Normalization factor	\(\kappa(x,\mu) = \mu\)	\(\mu\)	1
`shapefactor`, `staterror`	Shape factor	\(\kappa(x,\vec{\gamma}) = \chi_b^{\gamma}\)	\(\gamma_0\), ..., \(\gamma_n\)	#bins