About this document

---

To the extent possible under law, the authors have waived all copyright and related or neighboring rights to this document. For details, please refer to the Creative Commons CC0 license ². This work is published from: CERN, Geneva.

---

Introduction

This section is non-normative.

It is widely agreed upon that the publication of likelihood models from high energy physics experiments is imperative for the preservation and public access to these results. Detailed arguments have been made elsewhere already ³. This document sets out to provide a standardized format to publish and archive statistical models of any size and across a wide range of mathematical formalisms in a way that is readable by both humans and machines. With the introduction of pyhf ⁴⁵, a JSON format for likelihood serialization has been put forward. However, an interoperable format that encompasses likelihoods with a scope beyond stacks of binned histograms was lacking. With the release of ROOT 6.26/00 ⁶ and the experimental RooJSONFactoryWSTool therein, this gap has now been filled. This document sets out to document the syntax and features of the Statistics Serialization Standard (HS\({}^3\)) for likelihoods and statistical models in general, as to be adopted by any HS\({}^3\)-compatible statistics framework. The examples in this document employ the JSON notation, but are intended to encompass also representations as YAML or TOML.

How to use this document

Developers of statistical toolkits are invited to specifically refer to versions of this document relating to the support of this standard in their respective implementations. Please note that this document as well as the HS\({}^3\) standard are still in development and can still undergo minor and major changes in the future. This document describes the syntax of HS\({}^3\) v0.2.9.

Statistical semantics of HS\({}^3\)

Statistical models, probability distributions and parameters

HS\({}^3\) takes a "forward-modelling" approach throughout: a statistical model \(m\) maps a space \(\Theta\) of free parameters \(\theta\) to a space of probability distributions that describe the possible outcomes of a specific experiment. For any given parameters \(\theta\), the model returns a concrete probability distribution \(m(\theta)\). Observed data \(x\) is then treated as random variate, presumed to be drawn from the model: \(x \sim m(\theta)\). Parameters in HS\({}^3\) are always named, so semantically the elements of a parameter space \(\Theta\) are named tuples \(\theta\) (meaning tuples in which every entry has a name). Even if there is only a single free parameter, \(\theta\) should be thought of as a single-entry named tuple. In the current version of this standard, parameter tuples must be flat and only consist of real numbers, vector-valued or nested entries are not supported yet. Future versions of the standard will likely be less restrictive, especially with respect to discrete or vector-valued parameters. Parameter domains defined as part of this standard may be of various types, even though the current version only supports product domains. Future versions are likely to be less restrictive in this regard. Mathematically and computationally, it is often convenient to treat parameters as flat real-valued vectors instead of named tuples, it is the responsibility of the implementation to map between these different views of parameters when and where necessary. Probability distributions in HS\({}^3\) (see Distributions) are typically parameterized. Any instance of a distribution that has some of its parameters bound to names instead of concrete values, e.g. \(m = d_{\mu = a, \sigma = 0.7, \lambda = b, ...}\), constitutes a valid statistical model \(m(\theta)\) with model parameters \(\theta = (a, b)\). When probability distributions are combined via a Cartesian product (see Product distribution), then the named tuples that contain their free parameter values are concatenated. So \(m = d_{\mu = a, \sigma = b} \times d_{\mu = c, \sigma = 0.7}\) constitutes a model \(m(\theta)\) with model parameters \(\theta = (a, b, c)\). Distribution parameters may also be bound to the output of functions, and if those functions have inputs that are bound to names instead of values (or again bound to such functions, recursively), then those names become part of the model parameters. A configuration \(m = d_{\mu = a, \sigma = 0.7, \lambda = f}, f = \texttt{sum}(4.2, g), g = \texttt{sum}(1.3, b)\), for example, also constitutes a (different) model \(m(\theta)\) with parameters \(\theta = (a, b, c)\). If all parameter values of a probability distribution are set to concrete values, so if there are not directly (or indirectly via functions) bound to names, we call this probability distribution a concrete distribution here. Such distributions can be used as Bayesian priors (see Bayesian inference). The variates of all distributions (so the possible results of random draws from them) are also named tuples in all cases. So even instances of univariate distributions, like the normal distributions, have variates like \((x = \ldots)\). The names in the variate tuples can be configured for each instance of a distribution, and must be unique across all distributions that are used together in a model. In Cartesian products of distributions, their variate tuples are concatenated. As with parameter tuples, nested tuples are not supported. The tuple entries, however, may be vector-valued, in contrast to parameter tuples.

Probability density functions (PDFs)

Statistics literature often discriminates between probability density functions (PDF) for continuous probability distributions and probability mass functions (PMF) for discrete probability distributions. This standard use the term PDF for both continuous and discrete distributions. The concept of density is to be understood in terms of densities in the realm of measure theory here, that is the density of a probability measure (distribution) is its Radon-Nikodym derivative in respect to an (implied) reference measure. The choice of reference measure would be arbitrary in principle, which scales likelihood functions (Sec. Likelihood) by a constant factor that depends on choice of reference. In this standard, a specific reference measures is implied for each probability distribution, typically the Lebesgue measure for continuous distributions and the counting measure for discrete distributions. The standard aims to to match the PDF (resp. PMF) most commonly used in literature for each specific probability distribution and the mathematical form of the PDF is documented explicitly for each distribution in the standard. So within HS\({}^3\), probability densities and likelihood functions are unambiguous. Here we use \(\text{PDF}(m(\theta), x)\) to denote the density value of the probability distribution/measure \(m\), parameterized by \(\theta\), at the point/variate \(x\), in respect to the implied reference for \(m\).

Observed and simulated data

The term data refers here to any collection of values that represents the outcome of an experiment. Data takes the same form as variates of distributions (see Distributions, i. e. named tuple of real values or vectors. To compare given data with a given model, the names and shapes of the data entries must match the variates of the probability distributions \(m(\theta)\) that the model returns for a specific choice of parameters \(\theta\). This means that given a model \(m\) and concrete parameter values \(\theta\), drawing a set of random values from the probability distribution \(m(\theta)\) produces a valid set of simulated observations. Implementations can use this to provide mock-data generation capabilities.

Likelihood functions

The concrete probability distribution \(m(\theta)\) that a model \(m\) returns for specific parameter values \(\theta\) can be compared to observed data \(x\). This gives rise to a likelihood \(\mathcal{L}_{m,x}(\theta) = \text{PDF}(m(\theta), x)\) that is a real-valued function on the parameter space. Multiple distributions/models that describe different modes of observation can be combined with multiple sets of data that cover those modes of observation into a single likelihood (Sec. Likelihoods). In addition to using observed data, implementations may provide the option to use random data generated from the model (see Data) to check for Monte-Carlo closure.

Frequentist parameter inference

The standard method of frequentist inference is the maximum (or, respectively, profile) likelihood method. In the vast majority of cases, the test statistic used here is the likelihood ratio, that is, the ratio of two values of the likelihood corresponding to two different points in parameter space: one that maximizes the likelihood unconditionally, one one that maximizes the likelihood under some condition such as the values of the parameters of interest expected in the absence of a deviation from the null hypothesis. The corresponding building blocks for such an analysis, such as the list of parameters of interest and the likelihood function to be used, are specified in the analysis section of an HS\({}^3\) configuration (Sec. Analyses).

Bayesian parameter inference

The standard also encompasses the specification of Baysian posterior distributions over parameters by combining (Sec. Analyses) likelihoods with probabilty distributions that acts the priors. Here concrete distributions are used to describe the prior probability of parameters in addition to parameterized distributions that are used to describe of the probability of observing specific data.

How to read this document

In the context of this document, any JSON object is referred to as a struct. A key-value-pair inside such a struct is referred to as a component. If not explicitly stated otherwise, all components mentioned are mandatory. The components located inside the top-level struct are referred to as top-level components. The keywords optional and required, as well as should and may are used in accordance with IETF requirement levels ⁷.

Terms and Types

This is a list of used types and terms in this document.

• struct: represented with { }, containing a key:value mapping, keys are of type string.
• component: key-value pair within a struct
• array array of items (either strings or numbers) without keys. Represented with [...].
• string: references to objects, names and arbitrary information. Represented with
• number: either floating or integer type values
• boolean: boolean values; they can be encoded as true and false

All structs defining functions, distributions, parameters, variables, domains, likelihoods, data or parameter points will be referred to as objects. All objects must always have a component name that must be unique among all objects.

Within most top-level components, any one string given as a value to any component should refer to the name of another object, unless explicitly stated otherwise. Top-level components in which this is not the case are explicitly marked as such.

File format

HS\({}^3\) documents are encoded in the JSON format as defined in ISO/IEC 21778:2017 ⁸. Implementations may support other serialization formats that support a non-ambiguous mapping to JSON, such as TOML or YAML, in which case they should use a different file extension.

Validators

Future versions of this standard will recommend official validator implementations and schemata. Currently, these have not been finalized.

How to get in touch

Visit the GitHub page https://github.com/hep-statistics-serialization-standard/hep-statistics-serialization-standard

Top-level components

In the following, the top-level components of HS\(^3\) and their parameters/arguments are described. Each component is completely optional, but certain components may depend on other components, which should be provided in that case. The only exception is the component metadata containing the version of HS\(^3\), which is always required. The supported top-level components are

• distributions: (optional) array of objects defining distributions
• functions: (optional) array of objects defining mathematical functions
• data: (optional) array of objects defining observed or simulated data
• likelihoods: (optional) array of objects defining combinations of distributions and data
• domains: (optional) array of objects defining domains, describing ranges of parameters
• parameter_points: (optional) array of objects defining parameter points. These may be used as starting points for minimizations or to document best-fit-values or nominal truth values of datasets
• analyses: (optional) array of objects defining suggested analyses to be run on the models in this file
• metadata: required struct containing meta information; HS\(^3\) version number (required), authors, paper references, package versions, data/analysis descriptions (optional)
• misc: (optional) struct containing miscellaneous information, e.g. optimizer settings, plotting colors, etc.

In the following each of these are described in more detail with respect to their own structure.

Distributions

The top-level component distributions contains an array of distributions in struct format. Distributions must be normalized, thus, the letter \(\ensuremath{\mathcal{M}}\) in the following descriptions will always relate to the normalization of the distribution. The value of \(\ensuremath{\mathcal{M}}\) is conditional on the current domain. It must be chosen such that the integral of the distribution over the current domain equals one. The implementations might chose to perform this integral using analytical or numerical means. Each distribution must have the components type, denoting the kind of distribution described, and a component name, which acts as a unique identifier of this distribution among all other named objects. Distributions in general have the following keys: - name: custom unique string (required), e. g. my_distribution_of_x - type: string (required) that determines the kind of distribution, e. g. gaussian_dist - ...: each distribution may have components for the various individual parameters. For example, distributions of type gaussian_dist have the specific components mean, sigma and x. In general, these components may be strings as references to other objects, but may also directly yield numeric or boolean values. Depending on the parameter and the type of distribution, they appear either in single item or array format.

Example: Distributions

"distributions":[
    { 
        "name":"gauss1", 
        "type":"gaussian_dist", 
        "mean":1.0, 
        "sigma":"param_sigma", 
        "x":"param_x" 
    }, 
    { 
        "name":"exp1", 
        "type":"exponential_dist", 
        "c":-2, 
        "x":"data_x" 
    }, 
    ... 
] 

Distributions can be treated either as extended or as non-extended ⁹. Some distributions are always extended, others can never be extended, yet others can be used in extended and non-extended scenarios and have a switch selecting between the two. An non-extended distribution is always normalized to the unity. An extended distribution, on the other hand, can yield values larger than unity, where the yield is interpreted as the number of predicted events. That is to say, the distribution is augmented by a factor that is a Poisson constraint term for the total number of events. In the following, all distributions supported in HS\({}^3\) v0.2.9 are listed in detail. Future versions will expand upon this list.

Univariate fundamental distributions

This section contains univariate fundamental distributions in the sense that they cannot refer to any other distribution -- only to functions, parameters and exactly one variable.

Argus distribution

The Argus background distribution is defined as

\[ \begin{aligned} \text{ArgusPdf}(m, m_0, c, p) = \frac{1}{\ensuremath{\mathcal{M}}} \cdot m \cdot \left[ 1 - \left( \frac{m}{m_0} \right)^2 \right]^p \cdot \exp\left[ c \cdot \left(1 - \left(\frac{m}{m_0}\right)^2 \right) \right] \end{aligned} \]

and describes the ARGUS background shape.

• name: custom unique string
• type: argus_dist
• mass: name of the variable \(m\) used as mass
• resonance: value or name of the parameter used as resonance \(m_0\)
• slope: value or name of the parameter used as slope \(c\)
• power: value or name of the parameter used as exponent \(p\).

Continued Poisson distribution

The of a continued Poisson distribution of the variable \(x\) is defined as

\[ \begin{aligned} \text{ContinuedPoissonPdf}(x, \lambda) = \frac{1}{\ensuremath{\mathcal{M}}} \exp\left(x \cdot \ln \lambda - \lambda - \ln \Gamma(x+1)\right), \end{aligned} \]

where \(\Gamma\) denotes the Euler Gamma function.

This function is similar the the Poisson distribution (see Poisson distribution{reference-type="ref" reference="dist:poisson"}), but can accept non-integer values for \(x\). Notably, the differences between the two might be significant for small values of \(x\) (below x). Nevertheless, the distribution is useful to deal with datasets with non-integer event counts, such as asimov datasets ¹⁰.

• name: custom unique string
• type: poisson_dist
• x: name of the variable \(x\) (usually referred to as \(k\) for the standard integer case)
• mean: value or name of the parameter used as mean \(\lambda\).

Uniform distribution

The of a continuous uniform distribution is defined as:

\[ \begin{aligned} \text{UniformPdf}(x) = \frac{1}{\ensuremath{\mathcal{M}}} \end{aligned} \]

• name: custom unique string
• type: uniform_dist
• x: name of the variable \(x\)

CrystalBall distribution

The generalized Asymmetrical Double-Sided Crystall Ball line shape, composed of a Gaussian distribution at the core, connected with two powerlaw distributions describing the lower and upper tails, given by

\[ \begin{aligned} \text{CrystalBallPdf}(m;m_0,\sigma,\alpha_L,n_L,\alpha_R,n_R) = \frac{1}{\ensuremath{\mathcal{M}}} \begin{cases} A_L \cdot (B_L - \frac{m - m_0}{\sigma_L})^{-n_L}, & \mbox{for }\frac{m - m_0}{\sigma_L} < -\alpha_L \\ \exp \left( - \frac{1}{2} \cdot \left[ \frac{m - m_0}{\sigma_L} \right]^2 \right), & \mbox{for }\frac{m - m_0}{\sigma_L} \leq 0 \\ \exp \left( - \frac{1}{2} \cdot \left[ \frac{m - m_0}{\sigma_R} \right]^2 \right), & \mbox{for }\frac{m - m_0}{\sigma_R} \leq \alpha_R \\ A_R \cdot (B_R + \frac{m - m_0}{\sigma_R})^{-n_R}, & \mbox{otherwise}, \\ \end{cases} \end{aligned} \]

where

\[ \begin{aligned} A_i &= \left(\frac{n_i}{\left| \alpha_i \right|}\right)^{n_i} \cdot \exp\left(- \frac {\left| \alpha_i \right|^2}{2}\right) \\ B_i &= \frac{n_i}{\left| \alpha_i \right|} - \left| \alpha_i \right| \\ \end{aligned} \]

The keys are

• name: custom string
• type: crystalball_dist
• m: name of the variable \(m\)
• m0: name or value of the central value \(m_0\)
• alpha: value or names of \(\alpha_L\) and \(\alpha_R\) from above. must not be used in conjuction with alpha_L or alpha_R.
• alpha_L: value or names of \(\alpha_L\) from above. must not be used in conjuction with alpha.
• alpha_R: value or names of \(\alpha_R\) from above. must not be used in conjuction with alpha.
• n: value or names of \(n_L\) and \(n_R\) from above. must not be used in conjuction with n_L or n_R.
• n_L: value or names of \(n_L\) from above. must not be used in conjuction with n.
• n_R: value or names of \(n_R\) from above. must not be used in conjuction with n.
• sigma: value or names of \(\sigma_L\) and \(\sigma_R\) from above. must not be used in conjuction with sigma_L or sigma_R.
• sigma_L: value or names of \(\sigma_L\) from above. must not be used in conjuction with sigma.
• sigma_R: value or names of \(\sigma_R\) from above. must not be used in conjuction with sigma.

Exponential distribution

The exponential distribution is defined as

\[ \begin{aligned} \text{ExponentialPdf}(x, c) = \frac{1}{\ensuremath{\mathcal{M}}} \cdot \exp(-c\cdot x) \end{aligned} \]

• name: custom unique string
• type: exponential_dist
• x: name of the variable \(x\)
• c: value or name of the parameter used as coefficient \(c\).

Gaussian Normal distribution

The Gaussian/Normal distribution is defined as

\[ \begin{aligned} \text{GaussianPdf}(x, \mu, \sigma) = \frac{1}{\ensuremath{\mathcal{M}}} \exp\left(\frac{(x-\mu)^2}{\sigma^2}\right) \end{aligned} \]

• name: custom unique string
• type: gaussian_dist or normal_dist
• x: name of the variable \(x\)
• mean: value or name of the parameter used as mean value \(\mu\)
• sigma: value or name of the parameter encoding the standard deviation \(\sigma\).

Log-Normal distribution

The log-normal distribution is defined as

\[ \begin{aligned} \text{LogNormalPdf}(x, \mu, \sigma) &= \frac{1}{\ensuremath{\mathcal{M}}} \frac{1}{ x } \exp\left( -\frac{(\ln(x)-\mu)^2}{2\sigma^2}\right) \end{aligned} \]

• name: custom unique string
• type: lognormal_dist
• x: name of the variable \(x\)
• mu: value or name of the parameter used as \(\mu\)
• sigma: value or name of the parameter \(\sigma\) describing the shape

Poisson distribution

The Poisson distribution of the variable \(x\) is defined as

\[ \begin{aligned} \text{PoissonPdf}(x, \lambda) = \frac{1}{\ensuremath{\mathcal{M}}} \frac{\lambda^x}{x!} \text{e}^{-\lambda}. \end{aligned} \]

where \(x\) is required to be an integer. In this case, the behavior for non-integer values of \(x\) is undefined. - name: custom unique string - type: poisson_dist - x: name of the variable \(x\) (usually referred to as \(k\) for the standard integer case) - mean: value or name of the parameter used as mean \(\lambda\).

Polynomial distribution

The polynomial distribution is defined as

\[ \begin{aligned} \text{PolynomialPdf}(x, a_0, a_1, a_2, ...) = \frac{1}{\ensuremath{\mathcal{M}}} \sum_{i=0}^n a_i x^i = a_0 + a_1 x + a_2 x^2 + ... \end{aligned} \]

• name: custom unique string
• type: polynomial_dist
• x: name of the variable \(x\)
• coefficients: array of coefficients \(a_i\). The length of this array implies the degree of the polynomial.

Multivariate fundamental distributions

This section contains multivariate fundamental distributions. They may refer to functions, parameters and more than one variable.

Barlow-Besston-Lite Constraint distribution

This distribution represents a product of Poisson distributions defining the statistical uncertainties of the histogram templates defined in a histfactory_func.

\[ \begin{aligned} \text{BarlowBeestonLitePoissonConstraintPdf}(x) &= \frac{1}{\ensuremath{\mathcal{M}}} \prod_i^n \text{PoissonPdf}(x_i\cdot \tau_i,\tau_i) \end{aligned} \]

• name: custom unique string
• type: barlow_beeston_lite_poisson_constraint_dist
• x: name of the variable \(x\)
• expected: array of central values \(\tau_i\)

Multivariate normal distribution

The multivariate normal distribution is defined as

\[ \begin{aligned} \text{MvNormalPdf}(\mathbf{x}, \boldsymbol\mu, \boldsymbol\Sigma) &= \frac{1}{\ensuremath{\mathcal{M}}} \exp \left( -\frac{1}{2} (\mathbf{x} - \boldsymbol\mu)^{\!\mathsf{T}} \boldsymbol\Sigma^{-1}(\mathbf{x} - \boldsymbol\mu) \right), \end{aligned} \]

with \(\boldsymbol\Sigma \in \mathbb{R}^{k\times k}\) being positive-definite.

• name: custom unique string
• type: multivariate_normal_dist
• x: array of names of the variables \(\mathbf{x}\). This also includes mixed arrays of values and names.
• mean: array of length \(k\) of values or names of the parameters used as mean values \(\boldsymbol\mu\)
• covariances: an array comprised of \(k\) sub-arrays, each of which is also of length \(k\), designed to store values or names of the entries of the covariance matrix \(\boldsymbol\Sigma\). In general, the covariance matrix \(\boldsymbol\Sigma\) must be symmetric and positive semi-definite.

Note: Users should prefer the specific distributions defined in this standard over generic distributions where possible, as implementations of these will typically be more optimized. Generic distributions should only be used if no equivalent specific distribution is defined.

A generic distribution is defined by an expression that respresents the PDF of the distribution in respect to the Lebesque measure. The expression must be a valid HS³-expression string (see Section Generic Expressions).

• name: custom string
• type: generic_dist
• expression: a string with a generic mathematical expression. Simple mathematical syntax common to most programming languages should be used here, such as x-2*y+z. The arguments x, y and z in this example must be parameters, functions or variables. The distribution is normalized by the implementation, a normalization term should not be included in the expression. If the expression results in a negative value, the behavior is undefined.

HistFactory distribution

HistFactory ¹¹ is a language to describe statistical models consisting only of "histograms" (which is used interchangeably with "step-functions" in this context). Each HistFactory distribution describes one "channel" or "region" of a binned measurement, containing a stack of "samples", i. e. binned distributions sharing the same binning (step-functions describing the signal or background of a measurement). Such a HistFactory model is shown in Figure 1 (originally from ¹²). Each of the contributions may be subject to modifiers.

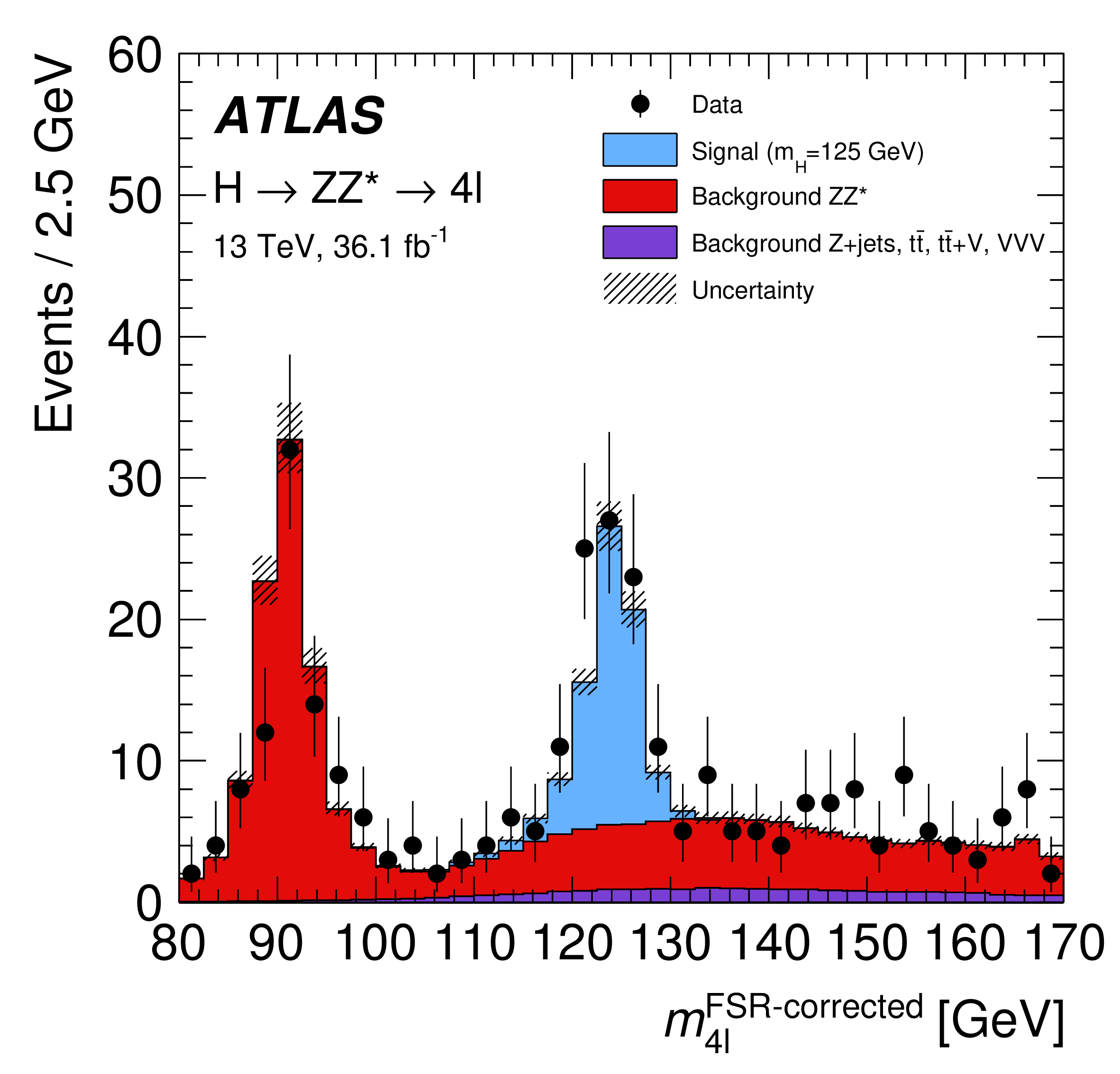
The prediction for a binned region is given as

\[ \begin{aligned} \lambda(x)=\sum_{s\in\text{samples}} \left[ \left( d_s(x) + \sum_{\delta\in M_{\delta}} \delta(x,\theta_\delta) \right) \prod_{\kappa\in M_\kappa} \kappa(x,\theta_\kappa) \right] \end{aligned} \]

Here \(d_s(x)\) is the prediction associated with the sample \(s\), a step function

\[ \begin{aligned} d_s(x) = \chi^{y_s}_{b}(x) \end{aligned} \]

In this section, \(\chi^{y_s}_{b}(x)\) denotes a generic step function in the binning \(b\) such that \(\chi_{b}(x) = y_{s,i}\), some constant, if \(x\in[b_i,b_{i+1})\). The \(y_{s,i}\) in this case are the bin contents (yields) of the histograms. The \(M_\kappa\) are the multiplicative modifiers, the \(M_\delta\) are the additive modifiers. Each of the modifiers is either multiplicative (\(\kappa\)) or additive (\(\delta\)). All samples and modifiers share the same binning \(b\). The modifiers depend on a set of nuisance parameters \(\theta\), where each modifier can only depend on one \(\theta_i\), but the \(\theta_i\) can take the form of vectors and the same \(\theta_i\) can be shared by several modifiers. By convention, these are denoted \(\alpha\) if they affect all bins in a correlated way, and \(\gamma\) if they affect only one bin at a time. The types of modifiers are

• A uncorrelated shape systematic or shapefactor modifier is a multiplicative modifier that scales each single bin by the value of some independent parameter \(\gamma\). Here, \(\theta_i=\vec{\gamma}\), where the length of \(\vec{\gamma}\) is equal to the number of bins in this region. This type of modifier is sometimes called shapesys, with some nuance in the meaning. However, both are synonymous in the context of this standard.
• A correlated shape systematic or histosys modifier is an additive modifier that adds or subtracts a constant step function \(\chi^f\), scaled with a single factor \(\alpha\). The modifier contains a data section, which contains the subsections \(\texttt{hi}\) and \(\texttt{lo}\) that help to define the step function \(\chi^f\). They contain contents, which define the bin-wise additions or subtractions for \(\alpha=1\). Here, \(\theta_i=\alpha\).
• A normalization systematic or normsys modifier is a multiplicative modifier that scales the entire sample with the same constant factor \(f\) that is a function of \(\alpha\). The modifier contains a data section, which contains the values \(\texttt{hi}\) and \(\texttt{lo}\) that help to define \(f\). There are different functional forms that can be chosen for \(f\). However, by convention \(f(\alpha=0)=1\), \(f(\alpha=+1)=\)"hi" and \(f(\alpha=-1)=\)"lo". In this case, \(\theta_i=\alpha\).
• A normalization factor or normfactor modifier is a multiplicative modifier that scales the entire sample in this region with the value of the parameter \(\mu\) itself. In this case, \(\theta_i=\mu\).
• The staterror modifier is a shorthand for encoding uncorrelated statistical uncertainties on the values of the step-functions, using a variant¹ of the Barlow-Beeston Method ¹³. Here, the relative uncertainty on the sum of all samples in this region containing the staterror modifier is computed bin-by-bin. Then, a constrained uncorrelated shape systematic (shapesys) is created, encoding these relative uncertainties in the corresponding Poisson (or Gaussian) constraint term.

The different modifies and their descriptions are also summarized in the following table:

Type of Modifier	Description	Definition	Free Parameters	Number of Free Parameters
histosys	Correlated Shape systematic	\(\delta(x,\alpha) = \alpha * \chi_b^f\)	\(\alpha\)	1
normsys	Normalization systematic	\(\kappa(x,\alpha) = f(\alpha)\)	\(\alpha\)	1
normfactor	Normalization factor	\(\kappa(x,\mu) = \mu\)	\(\mu\)	1
shapefactor, staterror	Shape factor	\(\kappa(x,\vec{\gamma}) = \chi_b^{\gamma}\)	\(\gamma_0\), ..., \(\gamma_n\)	#bins

The staterror modifier is a special subtype of shapefactor, where the mean of the constraint is given as the sum of the predictions of all the samples carrying a staterror modifier in this bin. The way modifiers affect the yield in the corresponding bin is subject to an interpolation function. The overallsys and histosys modifiers thus allow for an additional key interpolation, which identifies one of the following functions:

• lin: \(\begin{cases} y_{\textit{nominal}} + x \cdot (y_{\textit{high}} - y_{\textit{nominal}}) \text{ if } x\geq0\\ y_{\textit{nominal}} + x \cdot (y_{\textit{nominal}} - y_{\textit{low}}) \text{ if } x<0 \end{cases}\)
• log: \(\begin{cases} y_{\textit{nominal}} \cdot \left(\frac{y_{\textit{high}}}{y_{\textit{nominal}}}\right)^x \text{ if } x\geq0\\ y_{\textit{nominal}} \cdot \left(\frac{y_{\textit{low}}}{y_{\textit{nominal}}}\right)^{-x}\text{ if } x<0 \end{cases}\)
• parabolic: \(\begin{cases} y_{\textit{nominal}} + (2s+d)\cdot(x-1)+(y_{\textit{high}} - y_{\textit{nominal}}) \text{ if } x>1\\ y_{\textit{nominal}} - (2s-d)\cdot(x+1)+(y_{\textit{low}} - y_{\textit{nominal})}\text{ if } x<-1\\ s \cdot x^2 + d\cdot x \text{ otherwise} \end{cases}\) with \(s=\frac{1}{2}(y_{\textit{high}} + y_{\textit{low}}) - y_{\textit{nominal}}\) and \(d=\frac{1}{2}(y_{\textit{high}} - y_{\textit{low}})\)
• poly6: \(\begin{cases} y_{\textit{nominal}} + x \cdot (y_{\textit{high}} - y_{\textit{nominal}}) \text{ if } x>1\\ y_{\textit{nominal}} + x \cdot (y_{\textit{nominal}} - y_{\textit{low}}) \text{ if } x<-1\\ y_{\textit{nominal}} + x \cdot (S + x \cdot A \cdot (15 + x^2 \cdot (3x^2-10))) \text{ otherwise} \end{cases}\) with \(S = \frac{1}{2}(y_{\textit{high}} - y_{\textit{low}})\) and \(A=\frac{1}{16}(y_{\textit{high}} + y_{\textit{low}} - 2\cdot y_{\textit{nominal}})\)

Modifiers can be constrained. This is indicated by the component constraint, which identifies the type of the constraint term. In essence, the likelihood picks up a penalty term for changing the corresponding parameter too far away from its nominal value. The nominal value is, by convention, defined by the type of constraint, and is 0 for all modifiers of type sys (histosys, normsys) and is 1 for all modifiers of type factor (normfactor, shapefactor). The strength of the constraint is always such that the standard deviation of constraint distribution is \(1\).

The supported constraint distributions, also called constraint types, are Gauss for a gaussian with unit width (a gaussian distribution with a variance of \(1\)), Poisson for a unit Poissonian (e.g. a continous Poissonian with a central value 1), or LogNormal for a unit LogNormal,. If a constraint is given, a corresponding distribution will be considered in addition to the aux_likelihood section of the likelihood, constraining the parameter to its nominal value.

An exception to this is provided by the staterror modifier as described above, and the shapesys for which a Poissonian constraint is defined with the central values defined as the squares of the values defined in vals.

The components of a HistFactory distribution are:

• name: custom unique string
• type: histfactory_yield
• axes: array of structs representing the axes. If given each struct needs to have the component name. Further, (optional) components are max, min and nbins, or, alternatively, edges. The definition of the axes follows the format for binned data (see Section Binned Data).
• samples: array of structs containing the samples of this channel. For details see below. Struct of one sample:
• name: (optional) custom string, unique within this function
• data: struct containing the components contents and errors, depicting the data contents and their errors. Both components are arrays of the same length.
• modifiers: array of structs with each struct containing a component type of the modifier, as well as a component parameter (defining a string) or a component parameters (defining an array of strings) relating to the name or names of parameters controlling this modifier. Further (optional) components are data and constraint, both depending on the type of modifier. For details on these components, see the description above. Two modifiers are correlated exactly if they share the same parameters as indicated by parameter or parameters. In such a case, it is mandatory that they share the same constraint term. If this is not the case, the behavior is undefined.

HistFactory

{
  "name": "myAnalysisChannel",
  "type": "histfactory_dist",
  "axes": [ 
    { "max": 1.0, "min": 0.0, "name": "myRegion", "nbins": 2 } 
  ],
  "name":"myChannel1",
  "samples": [
    { 
      "name": "mySignal",
      "data": { "contents": [ 0.5, 0.7 ], "errors": [ 0.1, 0.1 ] },
      "modifiers": [
        { "parameter": "Lumi", "type": "normfactor" },
        { "parameter": "mu_signal_strength", "type": "normfactor" },
        { "constraint": "Gauss", "data": { "hi": 1.1, "lo": 0.9 }, 
          "parameter": "my_normalization_systematic_1", 
          "type": "normsys" },
        { "constraint": "Poisson", "type": "staterror", 
          "parameters": ["gamma_stat_1","gamma_stat_2"]},
        { "constraint": "Gauss", "type": "histosys", 
          "data": { 
            "hi": { "contents": [ -2.5, -3.1 ] }, 
            "lo": { "contents": [ 2.2, 3.7 ] } 
           }, 
           "parameter": "my_correlated_shape_systematic_1" },
        { "constraint": "Poisson", "data": { "vals": [ 0.0, 1.2 ] }, 
          "parameter": "my_uncorrelated_shape_systematic_2", 
          "type": "shapesys" }
      ]
    },
    { 
      "name": "myBackground",
      ... 
   }
  ]
} 

Relativistic Breit-Wigner distribution

The relativistic Breit-Wigner distribution describes the lineshape of a resonance studies in the mass spectrum of two particle system. It is assumed that the resonance can decay into a list of channels.

The first channel in the list indicates the system for which mass distribution is modelled.

\[ \begin{aligned} \label{eq:relativistic_breit_wigner_dist} \text{BreitWignerPDF}(m, m_\text{BW}) &= \frac{1}{\ensuremath{\mathcal{M}}}\frac{m \Gamma_1(m)}{\left|m_\text{BW}^2-m^2 - i m_\text{BW} \Gamma(m)\right|^2} ,\\ \nonumber \Gamma(m) &= \sum_i \Gamma_i(m) ,\\ \nonumber \end{aligned} \]

When modelling the mass spectrum, the term \(m\) in the numerator of Eq. (Breit-Wigner) accounts for a jacobian of transformation from \(m^2\) to \(m\). The width term \(\Gamma_1(m)\) adds for the phase space factor for the channel of interest

• name: custom unique string
• type: relativistic_breit_wigner_dist
• mass: name of the mass variable \(m_\text{BW}\)
• channels: list of structs encoding the channels

Each of the channels is defined by the partial width \(\Gamma_i(m)\), given as

\[ \begin{aligned} \Gamma_i(m) &= \Gamma_{\text{BW},i} n_{li}^2(m)\rho_i(m) ,\\ \nonumber \rho_i(m) &= 2q_i(m)/m ,\\ \nonumber q_i(m) &= \sqrt{(m^2-(m_{1i}+m_{2i})^2)(m^2-(m_{1i}-m_{2i})^2)} / (2m) ,\\ \nonumber n_{li}(m) &= z_i^{li}(m) h_{li}(z_i(m)) ,\\ \nonumber z_i(m) &= q_i(m)R_i \end{aligned} \]

The \(h_l(z)\) is the standard Blatt-Weisskopf form-factors, \(h_0^2(z) = 1/(1+z^2)\), \(h_1^2(z) = 1/(9+3z^2+z^4)\), and so on (Eqs.(50.30-50.35) in Ref. ¹⁴).\ The structs defining the channels should contain the following keys:

• name: name of the final state (optional)
• Gamma: partial width \(\Gamma_{\text{BW}}\) of the resonance
• m1: mass \(m_1\) of the first particle the resonance decays into (default value \(0\))
• m2: mass \(m_2\) of the second particle the resonance decays into (default value \(0\))
• l: orbital angular momentum \(l\) (default value \(0\))
• R: form-factor size parameter \(R\) (default value \(3\) GeV) For non-zero angular momentum, \(\Gamma_i(m_\text{BW})\) gives an approximation to the partial width of the resonance, not \(\Gamma_{\text{BW},i}\). A commonly used approximation of the relativistic Breit-Wigner function with the constant width is a special case of the Eq. (Breit-Wigner), where the [channels] argument contains a single channel with \(m_1=0\), \(m_2=0\), and \(l=0\).

Composite distributions

This section contains composite distributions in the sense that they refer to other distribution which they combine or modify in some way.

Mixture distribution

The mixture distribution, sometimes called addition of distributions, is a (weighted) sum of distributions \(f_i(\vec{x})\), depending on the same variable(s) \(\vec{x}\):

\[ \begin{aligned} \text{MixturePdf}(x) = \frac{1}{\ensuremath{\mathcal{M}}}\sum_{i=1}^{n} c_i \cdot f_i(\vec{x}) , \end{aligned} \]

where the \(c_i\) are coefficients and \(\vec{x}\) is the vector of variables.

• name: custom unique string
• type: mixture_dist
• name: name of the variable \(x\) (optional, since the variable is fully defined by the summands)
• summands: array of names referencing distributions
• coefficients: array of names of coefficients \(c_i\) or numbers to be added
• extended: boolean denoting whether this is an extended distribution (optional, as it can be inferred from the lengths of the lists for summands and coefficients) This distribution can be treated as extended or as non-extended.
• If the number of coefficients equals the number of distributions and extended is false, then the sum of the coefficient must be (approximately) one.
• If the number of coefficients equals the number of distributions and extended is true, then the sum of the coefficients will be used as the Poisson rate parameter and the mixture distribution itself will use the coefficients normalized by their sum.
• If the number of coefficients is one less than the number of distributions, then extended must be false and \(c_n\) is computed from the other coefficients as

\[ \begin{aligned} c_n &= 1 - \sum_{i=1}^{n-1}c_i . \end{aligned} \]

Product distribution

The product of s of independent distributions \(f_i\) is defined as

\[ \begin{aligned} \text{ProductPdf}(x) &= \frac{1}{\ensuremath{\mathcal{M}}}\prod_i^n f(x). \end{aligned} \]

• name: custom string
• type: product_dist
• x: name of the variable \(x\) (optional, since the variable is fully defined by the factors)
• factors: array of names referencing distributions

Density Function distribution

A distribution that is specified via a non-normalized density function \(f(x)\). Formally, it corresponds to the probability measure that has the density \(f(x)\) in respect to the Lebesgue measure.

The density function is normalized automatically by \(\ensuremath{\mathcal{M}}= \int f(x) dx\), so the PDF of the distribution is

\[ \begin{aligned} \text{DensityFunctionPdf}(f, x) &= \frac{f(x)}{\ensuremath{\mathcal{M}}} \end{aligned} \]

The distribution can be specified either via the non-normalized density function \(f(x)\) or via the non-normalized log-density function \(\log(f(x))\):

• density_function\_dist$: Specified via the PDF \(f(x)\)
• name: custom string
• type: density_function_dist
• function: The density function \(f\)
• log_density_function\_dist: Specified via the PDF \(f(x)\)
• name: custom string
• type: log_density_function_dist
• function: The density function \(f\)

Poisson point process

A Poisson point process distribution is understood here as the distribution of the outcomes of a (typically inhomogeneous) Poisson point process. In particle physics, such a distribution is often called an extended distribution ⁹. In HS³, a Poisson point process distribution is specified using a global-rate parameter \(\lambda\) and an underlying distribution \(m\), either explicitly or implicitly (see below). Random values are drawn from the Poisson point process distribution by drawing a random number \(n\) from a Poisson distribution of the global-rate \(\lambda\), and then drawing \(n\) random values from the underlying distribution \(m\). The resulting random values are vectors \(x\) of length \(n\), so their length varies. The PDF the Poisson point process distribution at an outcome \(x\) (a vector of length \(n\)) is

\[ \begin{aligned} \text{PoissonPointProcessPdf}(\lambda, m, x) &= \text{PoissonPdf}(n, \lambda) \cdot \prod_i^n \text{PDF}(m, x_i). \end{aligned} \]

In particle physics, the function \(\text{PoissonPointProcessPdf}(\lambda, m(\theta), x)\), for a fixed observation \(x\) and varying parameters \(\lambda\) and \(\theta\), is often called an extended likelihood. A a poisson point process distribution can be specified in HS³ in two ways:

• rate_extended_dist: The global-rate parameter \(\lambda\) and underlying distribution \(m\) are specified explicitly:
• name: custom string
• type: rate_extended_dist
• rate: The global rate \(\lambda\)
• dist: The underlying distribution \(m\)

The name of the variable \(x\) is taken from the underlying distribution. The underlying distribution must not be referred to from other components of the statistical model.

• rate_density_dist: Specified via a non-normalized rate-density function \(f\). Both the global-rate parameter and the underlying distribution are implicit: \(\lambda = \int f(y) d y\) and \(m = \text{DensityFunctionPdf}(f)\). More formally, the distribution corresponds to the inhomogeneous Poisson point process that is defined by a non-normalized rate measure which has density \(f\) in respect to the Lebesque measure.
• name: custom string
• type: rate_density_dist
• x: name of the variable \(x\)
• density: The rate-density function \(f\)

Bin count distribution

This is a binned version of the Poisson point process distribution (Poisson point process). Is is the distribution of the bin counts that result from histogramming the outcomes of a Poisson point process distribution using a given binning scheme (see Binned Data). Like the Poisson point process distribution, a Bin-counts distribution can either be specified via a global-rate parameter \(\lambda\) and an underlying distribution \(m\), or via a rate-density function \(f\) (in which case \(\lambda\) and \(m\) are implicit). In addition, the binning scheme also has to be specified in either case, unless it can be inferred (see below). For \(k\) bins, this type of distribution corresponds to a product of \(k\) Poisson distributions with rates

\[ \begin{aligned} \nu_i &= \lambda \cdot \int_{\text{bin}_i} \text{PDF}(y, m) dy \quad \text{equivalent to}\\ \nu_i &= \int_{\text{bin}_i} f(y) dy \end{aligned} \]

The PDF of the Bin-counts distribution at an outcome \(x\) (a vector of length \(k\), same as the number of bins) is

\[ \begin{aligned} \text{BinCountsPdf}(x) &= \prod_i^k \text{PoissonPdf}(x_i, \nu_i) \end{aligned} \]

• bincounts_extended_dist: The global-rate parameter \(\lambda\) and underlying distribution \(m\) are specified explicitly:
• name: custom string
• type: bincounts_extended_dist
• rate: The global rate \(\lambda\)
• dist: The underlying distribution \(m\)
• axes: a definition of the binning to be used, following the defintions in Binned data]. optional if dist is a binned distribution, in which case the same binning is used by default.

The name of the variable \(x\) is taken from the underlying distribution. The underlying distribution must not be referred to from other components of the statistical model. bincounts_density_dist: Specified via a non-normalized rate-density function \(f\). Both the global-rate parameter and the underlying distribution are implicit: \(\lambda = \int f(y) dy\) and \(m = \text{DensityFunctionPdf}(f)\).

More formally, the distribution corresponds to the inhomogeneous Poisson point process that is defined by a non-normalized rate measure which has density \(f\) in respect to the Lebesque measure.

• name: custom string
• type: bincounts_density_dist
• x: name of the variable \(x\)
• density: The rate-density function \(f\)
• axes: a definition of the binning to be used, following the defintions in Binned Data.

Functions

The top-level component functions describes an array of mathematical functions in struct format to be used as helper objects. Similar to distributions each entry is required to have the components type and name. Other components are dependent on the kind of functions. The field name is required and may be any custom unique string. Functions in general have the following components:

• name: custom unique string
• type: string that determines the kind of function, e.g. sum
• ...: each function has individual parameter keys for the various individual parameters. For example, functions of type sum have the parameter key summands. In general, these keys can describe strings as references to other objects or numbers. Depending on the parameter and the type of function, they appear either in single item or array format.

Example: Functions

"functions": [ 
    { 
        "name" : "sum1", 
        "type" : "sum", 
        "summands" : [1.8, 4, "param_xy"] 
    }, 
    ... 
]

In the following the implemented functions are described in detail.

Product

A product of values or functions \(a_i\).

\[ \begin{aligned} \text{Prod} &= \prod_i^n a_i \end{aligned} \]

• name: custom unique string
• type: product
• factors: array of names of the elements of the product or numbers.

Sum

A sum of values or functions \(a_i\).

\[ \begin{aligned} \text{Sum} &= \sum_i^n a_i \end{aligned} \]

• name: custom unique string
• type: sum
• summands: array of names of the elements of the sum or numbers.

Generic Function

Note: Users should prefer the specific functions defined in this standard over generic functions where possible, as implementations of these will typically be more optimized. Generic functions should only be used if no equivalent specific distribution is defined. A generic function is defined by an expression. The expression must be a valid HS³-expression string (see Section Generic Expressions).

• name: custom unique string
• type: generic_function
• expression: a string with a generic mathematical expression. Simple mathematical syntax common to programming languages should be used here, such as x-2*y+z. For any non-elementary operations, the behavior is undefined.

Data

The top-level component data contains an array of data sets in struct format. Each data set needs to contain the components type and name. Other components are dependent on the type of data set as demonstrated below:

• name: custom string
• type: string that determines the format of the observations
• ...: each type of observations has different parameter keys. Some of these are optional and marked accordingly in the more detailed description below

A detailed description of the different types with examples can be found below. While data, in most settings, has no uncertainty attached to it, this standard does allow to provide data with uncertainty, as there are some settings in which uncorrelated or correlated errors need to be taken into account. These include cases such as

• generated data obtained from importance sampling, including a (potentially Gaussian) uncertainty from the frequency weights
• unfolded data, resulting from arbitrarily complex transformation functions involving statistical models folding some degree of uncertainty into the data points themselves

While it should always be preferred to publish "raw" data, allowing to include pre-processed data with corresponding uncertainties expands the possible applications considerably.

Point Data

Point data describes a measurement of a single number, with a possible uncertainty (error).

• name: custom string
• type: point
• value: value of this data point
• uncertainty: (optional) uncertainty of this data point

Example: Point Data

"data":[ 
    { 
        "name":"data1", 
        "type":"point", 
        "value":0., 
        "uncertainty":1. 
    } 
]

Unbinned Data

Unbinned data describes a measurement of multiple data points in a possibly multi-dimensional space of variables. These data points can be weighted.

• name: custom string
• type: unbinned
• entries: array of arrays containing the coordinates/entries of the data
• axes: array of structs representing the axes. Each struct must have the components name as well as max and min.
• weights: (optional) array of values containing the weights of the individual data points, to be used for \(\chi^2\) comparisons and fits. If this component is not given, weight 1 is assumed for all data points. If given, the array needs to be of the same length as entries.
• entries_uncertainties: (optional) array of arrays containing the errors/uncertainties of each entry. If given, the array needs to be of the same shape as entries.
  Example: Unbinned Data

  "data":[ 
    { 
      "name":"data1", 
      "type":"unbinned", 
      "weights":[ 9.0, 18.4 ], 
      "entries":[ [1,3], [2,9] ], 
      "entries_uncertainties":[ [0.3], [0.6] ], 
      "axes":[ 
        { "name":"variable1", "min":1, "max":3 }, 
        { "name":"variable2", "min":-10, "max":10 }, 
        ... 
      ] 
    }, 
    ... 
  ]
  

Binned Data

Binned data describes a histogram of data points with bin contents in a possibly multi-dimensional space of variables. Whether entries that fall precisely on the bin boundaries are sorted into the smaller or larger bin is under the discretion of the creator of the model and thus not defined.

• name: custom string
• type: binned
• contents: array of values representing the contents of the binned data set
• axes: array of structs representing the axes. Each struct must have the component name. Further, it must specify the binning through one of these two options:
  1. regular binnings are specified through the components max, min and nbins
  2. potentially irregular binnings are specified through the component edges, which contains an array of length \(n+1\), where the first and last entries denote the minimum and and maximum of the variable, and all entries between denote the intermediate bin boundaries.
• uncertainty: (optional) struct representing the uncertainty of the contents. It consists of up to three components:
  • type: denoting the kind of uncertainty, for now only Gaussian distributed uncertainties denoted as gaussian_uncertainty are supported
  • sigma: array of the standard deviation of the entries in contents. Needs to be of the same length as contents
  • correlation: (optional) array of arrays denoting the correlation between the contents in matrix format. Must be of dimension length of contents \(\times\) length of contents. It can also be set to 0 to indicate no correlation.

Example: Binned Data

"data":[ 
  { 
    "name":"data2", 
    "type":"binned", 
    "contents":[ 9.0, 18.4 ], 
    "axes":[ { "name":"variable1", "nbins":2, "min":1, "max":3 } ] 
  }, 
  { 
    "name":"asimov_data2",
    "type":"binned", 
    "contents":[ 9.0, 18.4, 13, 0. ], 
    "axes":[ 
      { "name":"variable1", "nbins":2, "min":1, "max":3 }, 
      { "name":"variable2", "edges"[0,10,100] } 
    ] 
  }, 
    ... 
  ]

This type can also be used to store pre-processed data utilizing the uncertainty component

Example: Pre-processed binned Data

"data":[ 
  { 
    "name":"data4", 
    "type":"binned", 
    "contents":[ 9.0, 18.4 ], 
    "uncertainty" : { 
      "type": "gaussian_uncertainty", 
      "correlation" : 0, 
      "sigma" : [ 3, 4 ]
     }, 
    "axes":[ 
      { "name":"variable1", "nbins":2, "min":1, "max":3 }, 
      ... 
    ] 
  }, 
  ... 
] 

Likelihoods

The top-level component likelihoods contains an array of likelihoods in struct format specifying mappings of distributions and observations. The corresponding distributions and observations are inserted as keys in string format referencing to distributions and observations defined in the respective top-level components, or as numbers for fixed data values. The combination of parameterized distributions \(m_i(\theta_i)\) with observations \(x_i\) generates a likelihood function

\[ \begin{aligned} \ensuremath{\mathscr{L}}(\theta_1, \theta_2, \ldots) &= \prod_i \text{PDF}(m_i(\theta_i), x_i) \end{aligned} \]

The components of a likelihood struct are:

• name: custom string
• distributions: array of strings referencing the considered distributions
• data: array of strings referencing the used data, must be of the same length as the array of distributions. Alternatively, the data-values for single-dimensional distributions can be given in-line. For example, this can be used for constraint terms representing auxiliary measurements.
• aux_distributions: (optional) array of strings referencing the considered auxiliary distributions defined in the top-level component distributions. They can be used to encode regularizers or penalty terms to aid the minimization. These observed data for these distributions is implicit and not part of data.

Example: Likelihoods

"likelihoods":[ 
  { 
    "name":"likelihood1", 
    "distributions":[ 
      "dist1", 
      "dist2", 
      "single_dimensional_dist_1", 
      ... 
    ], 
    "data":         [ 
      "data1", 
      "data2", 
      0, 
      ... 
    ], 
    "aux_distributions" : [ "regularization_term" ] 
  }, 
  ... 
] 

Domains

The top-level component domains contains an array of domains giving information on the ranges of parameters and variables in struct format. Within a specified domain, the corresponding model is expected to yield valid values. Each domain must contain a name and a type although right now only the product_domain type is supported, even though others like e. g. a simplex domain might be added later. A domain consists of the following components:

• name: custom string
• type: product_domain
• axes: array of parameters and variables in this domain (see below) The component axes itself is an array of ranges each containing the components min, max and name.
• name: custom string
• max: upper bound of range
• min: lower bound of range

Example: Domains

"domains":[ 
  { 
    "name":"domain1", 
    "type":"product_domain", 
    "axes": [ 
      { "name" : "par_1", "max" : 1, "min" : 8 }, 
      { "name" : "par_2", "max" : 4.78, "min" : 6 }, 
      ... 
    ] 
  }, 
  ... 
]

Parameter points

The top-level component parameter_points contains an array of parameter configurations. These can be starting values for minimizations, parameter settings used to generate toy data, best-fit-values obtained, or points in parameter space used for different purposes.

• name: custom string
• parameters: array of parameter structs (see below) The component parameters is an array of components each containing:
• name: custom string
• value: number, value of variable
• const: (optional) boolean, whether variable is constant or not. Default is false.

Example: Parameter points

"parameter_points":[ 
  { 
    "name" : "starting_values", 
    "parameters": [ 
      { "name" : "par_1", "value": 3 }, 
      { "name" : "par_2", "value": 7, "const": true }, 
      ... 
     ] 
  }, 
  ... 
] 

Analyses

The top-level component analyses contains an array of possible (automated) analyses. To that extent, likelihoods, parameters of interest and the affiliated domains are listed. Description of the components:

• name: long custom string
• likelihood: name as reference to a likelihood defined in the top-level component likelihoods
• parameter_of_interest: (optional) array of names as reference to parameters that are interesting for the analysis at hand
• domain: name of a domain to be used for the parameters, defined in the top-level component domains
• init: (optional) name of an initial value to be used, defined in the top-level component parameter_points
• prior: (optional) name of a prior distribution, defined in the top-level component distributions. This is only used for Bayesian interpretations and should not be confused with auxiliary distributions listed in the likelihood section. The prior could, for example, be a product distribution of all the individual priors. If for any parameter, both a prior and a parameter domain are given, the prior should be truncated to the given parameter domain. Otherwise, implicit flat priors over the given parameter domain are assumed.

All parameters of all distributions in the likelihood must either be listed under the domain referenced, or set to const in the parameter point referenced.

Example: Analyses

"analyses": [ 
  { 
    "name" : "analysis1", 
    "likelihood" : "likelihood1", 
    "aux_likelihood_terms" : ["distribtion_1", "distribution_2", ...] 
    "parameters_of_interest" : ["param1"], 
    "domain" : "domain1" , 
    "init" : "starting_values", 
    "prior" : "prior_dist" 
  }, 
  ... 
]

Metadata

The top-level component metadata contains meta-information related to the creation of the file. The component hs3_version stores the HS\(^3\) version and is required for now. Overview of the components:

• hs3_version: (required) HS\(^3\) version number as String for reference
• packages: (optional) array of structs defining packages and their version number used in the creation of this file, depicted with the components name and version respectively
• authors: (optional) array of authors, either individual persons, or collaborations
• publications: (optional) array of document identifiers of publications associated with this file
• description: (optional) short abstract/description for this file

Example: Metadata

"metadata" : { 
  "hs3_version" : "0.2.0", 
  "packages" : [ { "name": "ROOT", "version": "6.28.02" } ], 
  "authors": ["The ATLAS Collaboration", "The CMS Collaboration"], 
  "publications": ["doiABCDEFG"]
} 

Miscellaneous

The top-level component misc can contain arbitrary, user-created information in struct format.

Example: Miscellaneous

"misc" : { 
  "customkey1" : "custom information 1" , 
  "myPackage_internal" : { 
    "somekey" : "custom info only affecting myPackage", 
    "default_color_for_all_curves" : "fuchsia" } 
  } 

This top-level component is intended to store any and all additional information, including user- or backend-specific meta-information. Examples include, but are not limited to:

• colors and styles for drawing distributions in this file
• suggested settings for samplers or minimizers when working with the distributions in this file
• comments explaining design choices made when building the model in this file
• suggested names and paths for output files to be used by backends working with this file

Supplementary Material

This section contains supplementary material referenced in section [sec:toplevel]

Generic Expressions

This section details the HS\({}^3\) generic expression language. Expressions can be use to specify generic functions and generic distributions. The implementations that support generic expression must support:

• Literal integer (format 1234), boolean (format TRUE and FALSE) and floating point (format 123.4, 1.234e2 and 1.234E2) values.
• Literal values for \(\pi\) (PI) and Euler's number (EULER).
• The arithmetic operators addition (x + y), subtraction (x - y), multiplication (x * y), division (x / y) and exponentiation (x^y).
• The comparison operators approximately-equal (x == y), exactly-equal (x === y), not-approximately-equal (x != y), not-exactly-equal (x !== y), less-than (x < y), less-or-equal (x <= y), greater-than (x >= y) and greater-or-equal (x >= y).
• The logical operators logical-inverse (!a), logical-and (a && b), logical-or (a || b), less-or-equal (a <= b), greater-than (a >= b) and greater-or-equal (a >= b).
• Round brackets to specify the order of operations.
• The ternary operator condition ? result_if_true : result_if_false
• The functions
  • exp(x): Euler's number raised to the power of x
  • log(x): Natural logarithm of x
  • sqrt(x): The square root of x
  • abs(x): The absolute value of x
  • pow(x, y): x raised to the power of y
  • pow(x, y): x raised to the power of y
  • min(x, y): minimum of x and y
  • max(x, y): maximum of x and y
  • sin(x): The sine of x
  • cos(x): The cosine of x
  • tan(x): The tangent of x
  • asin(x): The inverse sin of x
  • acos(x): The inverse cosine of x
  • atan(x): The inverse tangent of x

Symbols not defined here refer to variables in the HS\({}^3\) model. The operator precedence and associativity is acorrding to the common conventions. Spaces between operators and operands are optional. There must be no space between a function name and the function arguments, spaces between function arguments are optional (f(a, b) and f(a,b) are correct but f (a, b) is not allowed).

Division must be treated as floating-point division (i.e. 2/3 should be equivalent to 2.0/3.0).

The approximately-equal (a == b) and the not-approximately-equal operator (a != b), should compare floating-point numbers to within a small multiple of the unit of least precision. The behavior of any functions and operators not listed above is not defined, they are reserved for future versions of this standard. Implementations may support additional functions and operators as experimental features, but their use is considered non-standard and results in non-portable and potentially non-forward-compatible HS\({}^3\) documents.

References

---

1. The variation consists of summarizing all contributions in the stack to a single contribution as far as treatment of the statistical uncertainties is concerned. ↩

2. Creative Commons. Cc0 license. URL: https://creativecommons.org/publicdomain/zero/1.0. ↩

3. Kyle Cranmer, Sabine Kraml, Harrison Prosper, Philip Bechtle, Florian Bernlochner, Itay M. Bloch, Enzo Canonero, Marcin Chrzaszcz, Andrea Coccaro, Jan Conrad, Glen Cowan, Matthew Feickert, Nahuel Ferreiro, Andrew Fowlie, Lukas A. Heinrich, Alexander Held, Thomas Kuhr, Anders Kvellestad, Maeve Madigan, Farvah Nazila Mahmoudi, Knut Dundas Morå, Mark S. Neubauer, Maurizio Pierini, Juan Rojo, Sezen Sekmen, Luca Silvestrini, Veronica Sanz, Giordon H. Stark, Riccardo Torre, Robert Thorne, Wolfgang Waltenberger, Nicholas Wardle, and Jonas Wittbrodt. Publishing statistical models: getting the most out of particle physics experiments. SciPost Physics, January 2022. URL: http://dx.doi.org/10.21468/SciPostPhys.12.1.037, doi:10.21468/scipostphys.12.1.037. ↩

4. Lukas Heinrich, Matthew Feickert, and Giordon Stark. Pyhf. URL: https://github.com/scikit-hep/pyhf/releases/tag/v0.7.0, doi:10.5281/zenodo.1169739. ↩

5. Lukas Heinrich, Matthew Feickert, Giordon Stark, and Kyle Cranmer. Pyhf: pure-python implementation of histfactory statistical models. Journal of Open Source Software, 6(58):2823, 2021. URL: https://doi.org/10.21105/joss.02823, doi:10.21105/joss.02823. ↩

6. The ROOT Team. Root-project/root. March 2022. ↩

7. Scott O. Bradner. Key words for use in RFCs to Indicate Requirement Levels. RFC 2119, March 1997. URL: https://www.rfc-editor.org/info/rfc2119, doi:10.17487/RFC2119. ↩

8. The JSON data interchange syntax. ISO/IEC 21778, November 2017. URL: https://www.iso.org/standard/71616.html. ↩

9. Roger Barlow. Extended maximum likelihood. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 297(3):496–506, 1990. URL: https://www.sciencedirect.com/science/article/pii/0168900290913348, doi:https://doi.org/10.1016/0168-9002(90)91334-8. ↩↩

10. Glen Cowan, Kyle Cranmer, Eilam Gross, and Ofer Vitells. Asymptotic formulae for likelihood-based tests of new physics. Eur. Phys. J. C, 71:1554, 2011. [Erratum: Eur.Phys.J.C 73, 2501 (2013)]. arXiv:1007.1727, doi:10.1140/epjc/s10052-011-1554-0. ↩

11. Kyle Cranmer, George Lewis, Lorenzo Moneta, Akira Shibata, and Wouter Verkerke. HistFactory: A tool for creating statistical models for use with RooFit and RooStats. Technical Report, New York U., New York, January 2012. URL: https://cds.cern.ch/record/1456844. ↩

12. ATLAS Collaboration. Measurement of inclusive and differential cross sections in the $H \rightarrow ZZ^* \rightarrow 4\ell $ decay channel in \(pp\) collisions at \(\\sqrt s=13\) TeV with the ATLAS detector. JHEP, 10:132, 2017. arXiv:1708.02810, doi:10.1007/JHEP10(2017)132. ↩

13. Roger Barlow and Christine Beeston. Fitting using finite monte carlo samples. Computer Physics Communications, 77(2):219–228, 1993. URL: https://www.sciencedirect.com/science/article/pii/001046559390005W, doi:https://doi.org/10.1016/0010-4655(93)90005-W. ↩

14. R. L. Workman and Others. Review of Particle Physics. PTEP, 2022:083C01, 2022. doi:10.1093/ptep/ptac097. ↩